Da generazioni i Rothschild portano avanti una tradizione di mecenati eccezionale. Il loro grande interesse per la creatività e l'innovazione si è profuso in attività filantropiche uniche ed espresso in legami di amicizia intensi con artisti di grande fama..
Mayer Amschel Rothschild, fondatore della dinastia di famiglia, agli albori della Rivoluzione Francese, fu un collezionista di monete antiche. All'inizio del XIXmo secolo, il figlio maggiore riunì una meravigliosa collezione di opere d'arte a Francoforte e partecipò al movimento dell' Illuminismo in Europa.
L'elenco degli artisti che fecero parte della cerchia intima dei Rothschild è impressionante. Chopin fu, allo stesso tempo, amico e professore di Betty de Rothschild, il cui celeberrimo ritratto fu dipinto da Ingres. Mendelssohn diede lezione alle figlie piene di talento di Nathan Mayer Rothschild. Rossini frequentava James de Rothschild, e non esitava a rivolgersi al suo amico e banchiere per farsi offrire bottiglie di Château Lafite! Altri musicisti famosi quali Liszt, Paganini, Poulenc e Milhaud furono anch'essi accolti nella cerchia intima dei Rothschild. Infine, James de Rothschild ispirò personaggi a scrittori quali Balzac e Disraeli.
Edmond James de Rothschild, noto in Israele con il titolo di Benefattore, negli anni 30 offrì al Museo del Louvre la sua collezione di più di 40.000 incisioni e disegni antichi che aveva cominciato a collezionare all'età di cinque anni. Questi disegni, tra i quali si trovano opere di Leonardo da Vinci, Dürer e Rembrandt, continuano a suscitare l'ammirazione del pubblico del Louvre. Negli anni precedenti la Seconda Guerra Mondiale, il figlio di Edmond, Maurice svolse un ruolo fondamentale per il successo dei Grandi Balletti Russi e di Stravinsky a Parigi. Il suo unico erede, Edmond, l'eponimo fondatore dell'attuale Gruppo Edmond de Rothschild, nutriva un particolare interesse per l'arte francese del XVIII mo secolo. La stupenda « French Room » da lui donata al Museo d'Israele di Gerusalemme è un pezzo eccezionale che suscita l'ammirazione di ogni conservatore. Fu anche un generoso mecenate per la città di Ginevra, dove la famiglia risiede da più di 150 anni. Offrì al Museo d'Arte e Storia un dono senza precedenti: un vaso etrusco leggendario. Infine, Edmond riunì une collezione unica di oggetti inerenti al vino, con taluni pezzi che risalgono addirittura al Rinascimento. Una testimonianza che s'iscrive nella tradizione vitivinicola dei Rothschild.
Mecenati dei nostri tempi, Benjamin e Ariane de Rothschild continuano la trasmissione di tale eredità. Iscrivendosi nella modernità, incoraggiano l'innovazione, come testimonia la loro incomparabile collezione d'arte contemporanea. Sono altresì fortemente impegnati a sviluppare una rete filantropica internazionale, nell'ambito della quale l'arte è una componente essenziale, di pari passo con l'educazione. Pittura, musica, teatro e mestieri d'arte ne sono i principali pilastri. Si sono così creati partenariati con il Louvre, il Teatro dell'Odéon e la Scuola Boulle a Parigi, l'Accademia Bartabas a Versailles, il Museo Voltaire ed il Museo d'Arte e Storia a Ginevra e la Slade School of Fine Art a Londra. Infine, da molti anni sostengono il grande maestro spagnolo Jordi Savall nonché la celebre cantante Montserrat Figueras. Insieme, operano alla diffusione del dialogo tra le culture.
Citando Ariane de Rothschild: « L'arte e la musica condividono una virtù ammirevole, invitano al dialogo ed al ravvicinamento delle culture».
Dopo la Prima Guerra Mondiale, precisamente nel 1922 i Rothschild misero a disposizione fondi per la ricostruzione in numerosi paesi come Francia, Germania, Cecoslovacchia, Ungheria. A questo punto ho dovuto scacciare con la forza dalla mia mente un dubbio tremendo. E’ possibile che banchieri senza scrupoli fomentino a proprio piacimento le guerre, magari finanziando entrambe le fazioni e innescando la miccia fornendo poi i soldi per la ricostruzione? In via molto ipotetica sì. Scatenare una guerra non è così difficile: si forniscono le armi a entrambe le parti e si trova una motivazione sufficiente: religione, petrolio, terrorismo, ecc.
No! La perfidia umana non può arrivare a tanto! Giusto?
A questo punto negare o far finta di non vedere che l’impero dei Rothschild fin dai primi anni del secolo XIX ha influenzato la politica, l’economia e la finanza del mondo intero è un’offesa alla comune intelligenza.
E oggi? Come sono messi, anzi, visto che interessa pure la nostra cara Italia come siamo messi? Forse la famiglia si è ritirata a vita privata e si sta godendo un meritato riposo? Sbagliato. Certamente la vita è rimasta sempre molto privata. Non riesco infatti ancora a spiegarmi come la stampa, sempre più ricca di pettegolezzi e gossip e meno di informazioni utili, non s’interessi della vita di questi personaggi affascinanti e al limite del misterosofico.
Riescono –i media- a scovare una star televisiva che si sta abbronzando nuda dentro la caldera di un vulcano in pieno inverno e nessuno fa un servizio sugli appartenenti alla famiglia più potente del pianeta. Non è un po’ strano? Lungi da me l’idea che gli editor non possano fare servizi su certi banchieri internazionali, rimane allora la spiegazione che forse a nessuno interesserebbe. Strano perché personalmente preferirei leggere qualcosa su i «veri controllori» piuttosto che leggere e/o vedere qualche personaggetto estivo che pur di apparire nei giornali venderebbe la propria anima al diavolo, in questo caso fotografi e giornalisti.
Tornando al discorso di prima, oggi la famiglia Rothschild non ha perso prestigio e potere, semmai con il passare degli anni lo ha consolidato ulteriormente. Incredibile ma vero.Passano gli anni e i loro sistemi si adeguano. Oggi hanno sviluppato una divisione per il finanziamento d’impresa al servizio di fusioni e acquisizioni. Operazioni queste all’ordine del giorno. Basta aprire un qualsiasi giornale finanziario per leggere che la multinazionale ics si è unita, o è in procinto di farlo, con la transnazionale ipsilon. Fusioni il cui unico risultato è la creazione di megacorporazioni amministrate da pochissimi e composte da migliaia tra affiliate e holding. In fisica per innescare una fusione nucleare tra atomi serve molta energia qui le fusioni necessitano solo di soldi. Moltissimi soldi. Chi possiede tutti questi soldi se non i banchieri?
Vediamo adesso nel dettaglio dove i tentacoli economici dei Rothschild sono arrivati nel 3° Millennio. Per problemi di spazio cito solamente le società più conosciute e/o riguardanti il nostro paese, ma chiunque volesse approfondire consiglio di entrare nel sito ufficiale della famiglia e stamparsi l’elenco completo. Fate scorta di carta!
Tra le straniere spiccano: De Beers quella dei diamanti, la Enron fallita da poco, British Telecom, France Telecom, Deutch Telekom, Alcatel, Eircom, Mannesmann, AT&T, BBC, Petro China, Petro Bras, Canal +, Vivendi, Aventis, Unilever, Royal Canin, Pfaff, Deutch Post, e moltissime altre.
Torniamo adesso un momento in Italia poiché ce n’è per tutti i gusti: Tiscali, Seat Pagine Gialle, Eni, Rai, Banca di Roma, Banco di Napoli, BNL Banca Nazionale del Lavoro, Banca Intesa, Bipop-Carire, Banca Popolare di Lodi, Monte dei Paschi di Siena, Rolo Banca 1473, Finmeccanica. Vi può bastare? Penso proprio di sì!
Mi avvio a concludere nella speranza che questa piccola e incompleta illustrazione possa almeno aver fatto nascere qualche dubbio e/o curiosità in più su questa incredibile e decisamente atipica famigliola. Non posso confermare ma neppure smentire le pesanti e inquietanti affermazioni che svariati autori pubblicano sui Rothschild. Tengo a sottolineare che la cosa più incredibile è come i media in generale evitano di trattare tali argomentazioni. Passi il discorso sulla cospirazione globalizzata alla George Orwell, ma qui i fatti parlano chiaro.
Le trame e gli intrecci economici pure. Sono sotto gli occhi di tutti. Almeno di chi vuol vedere.
Non posso accontentarmi di leggere su La Stampa del 7 giugno 1996 che Lady Rothschild era l’ipotetica spia del KGB a Londra, o su Il Giornodel 29 agosto 2000 la cronaca della morte per overdose all’età di 23 anni di Raphael figlio di Nathaniel Rothschild.
Queste rientrano nel deleterio e purtroppo tanto seguito gossip.
Le cose serie e importanti sono altre.
 Ha l’aspetto molto poco rassicurante: assomiglia a un rettile preistorico. Ha una colorazione blu – grigia scura, talvolta bruno – grigiastra, con 9 – 12 bande verticali più scure sui 2 / 3 superiori del corpo e sulla dorsale. Quando non caccia vive nelle buie grotte oppure negli anfratti tra gli scogli. Questo animale è della famiglia degli anaricadidi che è rappresentata da 5 specie, tre delle quali vivono nell’Atlantico settentrionale. Le sue poderose mascelle fanno rabbrividire. Secondo gli studiosi in realtà è innocuo. Se la prende solamente con i ricci e i molluschi, che tritura coi suoi grandi molari.
Ha l’aspetto molto poco rassicurante: assomiglia a un rettile preistorico. Ha una colorazione blu – grigia scura, talvolta bruno – grigiastra, con 9 – 12 bande verticali più scure sui 2 / 3 superiori del corpo e sulla dorsale. Quando non caccia vive nelle buie grotte oppure negli anfratti tra gli scogli. Questo animale è della famiglia degli anaricadidi che è rappresentata da 5 specie, tre delle quali vivono nell’Atlantico settentrionale. Le sue poderose mascelle fanno rabbrividire. Secondo gli studiosi in realtà è innocuo. Se la prende solamente con i ricci e i molluschi, che tritura coi suoi grandi molari. Questo pesce è molto ricercato per la sua carne. Si ciba esclusivamente di crostacei e ricci di mare. Il pesce lupo può raggiungere un peso di 25 kg. ma si incontrano principalmente esemplari fra 3 e 10 Kg. Questo pesce ha un discreto interesse commerciale, soprattutto nel Nord Europa; commercializzato intero, decapitato o in filetti, sia fresco che congelato e talvolta affumicato; la sua pelle, piuttosto spessa, può essere lavorata come cuoio.
Questo pesce è molto ricercato per la sua carne. Si ciba esclusivamente di crostacei e ricci di mare. Il pesce lupo può raggiungere un peso di 25 kg. ma si incontrano principalmente esemplari fra 3 e 10 Kg. Questo pesce ha un discreto interesse commerciale, soprattutto nel Nord Europa; commercializzato intero, decapitato o in filetti, sia fresco che congelato e talvolta affumicato; la sua pelle, piuttosto spessa, può essere lavorata come cuoio. Ha l’aspetto molto poco rassicurante: assomiglia a un rettile preistorico. Ha una colorazione blu – grigia scura, talvolta bruno – grigiastra, con 9 – 12 bande verticali più scure sui 2 / 3 superiori del corpo e sulla dorsale. Quando non caccia vive nelle buie grotte oppure negli anfratti tra gli scogli. Questo animale è della famiglia degli anaricadidi che è rappresentata da 5 specie, tre delle quali vivono nell’Atlantico settentrionale. Le sue poderose mascelle fanno rabbrividire. Secondo gli studiosi in realtà è innocuo. Se la prende solamente con i ricci e i molluschi, che tritura coi suoi grandi molari.
Ha l’aspetto molto poco rassicurante: assomiglia a un rettile preistorico. Ha una colorazione blu – grigia scura, talvolta bruno – grigiastra, con 9 – 12 bande verticali più scure sui 2 / 3 superiori del corpo e sulla dorsale. Quando non caccia vive nelle buie grotte oppure negli anfratti tra gli scogli. Questo animale è della famiglia degli anaricadidi che è rappresentata da 5 specie, tre delle quali vivono nell’Atlantico settentrionale. Le sue poderose mascelle fanno rabbrividire. Secondo gli studiosi in realtà è innocuo. Se la prende solamente con i ricci e i molluschi, che tritura coi suoi grandi molari. Questo pesce è molto ricercato per la sua carne. Si ciba esclusivamente di crostacei e ricci di mare. Il pesce lupo può raggiungere un peso di 25 kg. ma si incontrano principalmente esemplari fra 3 e 10 Kg. Questo pesce ha un discreto interesse commerciale, soprattutto nel Nord Europa; commercializzato intero, decapitato o in filetti, sia fresco che congelato e talvolta affumicato; la sua pelle, piuttosto spessa, può essere lavorata come cuoio.
Questo pesce è molto ricercato per la sua carne. Si ciba esclusivamente di crostacei e ricci di mare. Il pesce lupo può raggiungere un peso di 25 kg. ma si incontrano principalmente esemplari fra 3 e 10 Kg. Questo pesce ha un discreto interesse commerciale, soprattutto nel Nord Europa; commercializzato intero, decapitato o in filetti, sia fresco che congelato e talvolta affumicato; la sua pelle, piuttosto spessa, può essere lavorata come cuoio.

![f:[a,b] \to \R \!](http://upload.wikimedia.org/math/1/1/9/119669a0a2241f66a809f34ce1d850f9.png) una funzione continua, allora
una funzione continua, allora 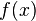 assume massimo e minimo nell'intervallo
assume massimo e minimo nell'intervallo ![[a,b] \!](http://upload.wikimedia.org/math/5/2/d/52d4fce11e59f0395730bb90f9b239cc.png) .
. è una funzione continua, essa trasforma insiemi compatti in insiemi compatti. Dato che
è una funzione continua, essa trasforma insiemi compatti in insiemi compatti. Dato che ![s = \sup(f[a,b])](http://upload.wikimedia.org/math/a/d/8/ad815f44d089ecd872c07fdb88df510d.png) e individuiamo una successione
e individuiamo una successione ![y_n \in f[a,b]](http://upload.wikimedia.org/math/d/c/8/dc8cf02d568df216b1a03df6f4165b18.png) tale che
tale che 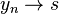 per
per  . Questa successione certamente esiste, infatti, se ciò non fosse vero nessuna successione convergerebbe ad
. Questa successione certamente esiste, infatti, se ciò non fosse vero nessuna successione convergerebbe ad  , e d'altra parte, essendo
, e d'altra parte, essendo ![y_n \in f([a,b])](http://upload.wikimedia.org/math/e/3/2/e3254cff63997764fa653ba9a33204c8.png) allora
allora ![\exists \tilde{x}\in[a,b]:f(\tilde{x})=y_n](http://upload.wikimedia.org/math/7/0/e/70e6600fc8e23e591054279dd05319b9.png) per cui avremmo
per cui avremmo ![\exists \epsilon > 0 \; \exists \tilde{x} \in [a,b] : f(\tilde{x}) \ge s+\epsilon>s \; \lor \; f(\tilde{x}) \le s-\epsilon](http://upload.wikimedia.org/math/e/4/c/e4c63c05bb2b5da719d536a59a975b75.png) cioè
cioè ![s\ne \sup(f[a,b])](http://upload.wikimedia.org/math/a/0/1/a010cf323783ddfffb2ed8412aa398ec.png) in contraddizione con le ipotesi.
in contraddizione con le ipotesi.![t_n \in [a,b]](http://upload.wikimedia.org/math/f/7/5/f751b0c29458ad8da51b9a271ce623b9.png) tale che
tale che  che converge verso
che converge verso ![x_2 \in [a,b]](http://upload.wikimedia.org/math/8/1/b/81bf19383e8ed5a5676f94b71900b44a.png) .
. per
per 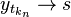 per
per 

![$\displaystyle det(A)=a_{11}[\sum (-1)^{r}\prod_{j=2}^{n}a_{ji_{j}}]+a_{12}[\sum
(-1)^{r}\prod a_{ji_{j}}]+...$](http://www.fisicict.altervista.org/res/dedo/pub/geometria/img965.gif)




