Sia ![f:[a,b] \to \R \!](http://upload.wikimedia.org/math/1/1/9/119669a0a2241f66a809f34ce1d850f9.png) una funzione continua, allora
una funzione continua, allora 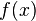 assume massimo e minimo nell'intervallo
assume massimo e minimo nell'intervallo ![[a,b] \!](http://upload.wikimedia.org/math/5/2/d/52d4fce11e59f0395730bb90f9b239cc.png) .
.
 è una funzione continua, essa trasforma insiemi compatti in insiemi compatti. Dato che
è una funzione continua, essa trasforma insiemi compatti in insiemi compatti. Dato che ![[a,b] \!](http://upload.wikimedia.org/math/5/2/d/52d4fce11e59f0395730bb90f9b239cc.png) è un intervallo chiuso e limitato per il teorema di Heine-Borel, è un compatto e quindi anche la sua immagine mediante
è un intervallo chiuso e limitato per il teorema di Heine-Borel, è un compatto e quindi anche la sua immagine mediante  sarà un compatto. Di conseguenza, il codominio di
sarà un compatto. Di conseguenza, il codominio di  ammetterà massimo e minimo.
ammetterà massimo e minimo.
![s = \sup(f[a,b])](http://upload.wikimedia.org/math/a/d/8/ad815f44d089ecd872c07fdb88df510d.png) e individuiamo una successione
e individuiamo una successione ![y_n \in f[a,b]](http://upload.wikimedia.org/math/d/c/8/dc8cf02d568df216b1a03df6f4165b18.png) tale che
tale che 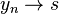 per
per  . Questa successione certamente esiste, infatti, se ciò non fosse vero nessuna successione convergerebbe ad s, in altre parole, per qualunque yn si avrebbe che
. Questa successione certamente esiste, infatti, se ciò non fosse vero nessuna successione convergerebbe ad s, in altre parole, per qualunque yn si avrebbe che  , e d'altra parte, essendo
, e d'altra parte, essendo ![y_n \in f([a,b])](http://upload.wikimedia.org/math/e/3/2/e3254cff63997764fa653ba9a33204c8.png) allora
allora ![\exists \tilde{x}\in[a,b]:f(\tilde{x})=y_n](http://upload.wikimedia.org/math/7/0/e/70e6600fc8e23e591054279dd05319b9.png) per cui avremmo
per cui avremmo ![\exists \epsilon > 0 \; \exists \tilde{x} \in [a,b] : f(\tilde{x}) \ge s+\epsilon>s \; \lor \; f(\tilde{x}) \le s-\epsilon](http://upload.wikimedia.org/math/e/4/c/e4c63c05bb2b5da719d536a59a975b75.png) cioè
cioè ![s\ne \sup(f[a,b])](http://upload.wikimedia.org/math/a/0/1/a010cf323783ddfffb2ed8412aa398ec.png) in contraddizione con le ipotesi.
in contraddizione con le ipotesi.
Scegliamo, inoltre, una successione![t_n \in [a,b]](http://upload.wikimedia.org/math/f/7/5/f751b0c29458ad8da51b9a271ce623b9.png) tale che f(tn) = yn.
tale che f(tn) = yn.
Per il teorema di Bolzano - Weierstrass (tn) ha una sottosuccessione che converge verso
che converge verso ![x_2 \in [a,b]](http://upload.wikimedia.org/math/8/1/b/81bf19383e8ed5a5676f94b71900b44a.png) .
.
Per la continuità di f abbiamo per
per  .
.
D'altra parte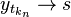 per
per  .
.
Quindi per l'unicità del limite abbiamo s = f(x2), cioè la funzione ha in x2 un massimo assoluto.
Similmente si dimostra anche l'esistenza di un punto x1 dove la funzione assume il valore minimo.
![f:[a,b] \to \R \!](http://upload.wikimedia.org/math/1/1/9/119669a0a2241f66a809f34ce1d850f9.png) una funzione continua, allora
una funzione continua, allora 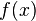 assume massimo e minimo nell'intervallo
assume massimo e minimo nell'intervallo ![[a,b] \!](http://upload.wikimedia.org/math/5/2/d/52d4fce11e59f0395730bb90f9b239cc.png) .
.Dimostrazione con la nozione di compattezza
Poiché è una funzione continua, essa trasforma insiemi compatti in insiemi compatti. Dato che
è una funzione continua, essa trasforma insiemi compatti in insiemi compatti. Dato che ![[a,b] \!](http://upload.wikimedia.org/math/5/2/d/52d4fce11e59f0395730bb90f9b239cc.png) è un intervallo chiuso e limitato per il teorema di Heine-Borel, è un compatto e quindi anche la sua immagine mediante
è un intervallo chiuso e limitato per il teorema di Heine-Borel, è un compatto e quindi anche la sua immagine mediante  sarà un compatto. Di conseguenza, il codominio di
sarà un compatto. Di conseguenza, il codominio di  ammetterà massimo e minimo.
ammetterà massimo e minimo.[modifica] Dimostrazione con successioni di punti
Poniamo![s = \sup(f[a,b])](http://upload.wikimedia.org/math/a/d/8/ad815f44d089ecd872c07fdb88df510d.png) e individuiamo una successione
e individuiamo una successione ![y_n \in f[a,b]](http://upload.wikimedia.org/math/d/c/8/dc8cf02d568df216b1a03df6f4165b18.png) tale che
tale che 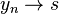 per
per  . Questa successione certamente esiste, infatti, se ciò non fosse vero nessuna successione convergerebbe ad s, in altre parole, per qualunque yn si avrebbe che
. Questa successione certamente esiste, infatti, se ciò non fosse vero nessuna successione convergerebbe ad s, in altre parole, per qualunque yn si avrebbe che  , e d'altra parte, essendo
, e d'altra parte, essendo ![y_n \in f([a,b])](http://upload.wikimedia.org/math/e/3/2/e3254cff63997764fa653ba9a33204c8.png) allora
allora ![\exists \tilde{x}\in[a,b]:f(\tilde{x})=y_n](http://upload.wikimedia.org/math/7/0/e/70e6600fc8e23e591054279dd05319b9.png) per cui avremmo
per cui avremmo ![\exists \epsilon > 0 \; \exists \tilde{x} \in [a,b] : f(\tilde{x}) \ge s+\epsilon>s \; \lor \; f(\tilde{x}) \le s-\epsilon](http://upload.wikimedia.org/math/e/4/c/e4c63c05bb2b5da719d536a59a975b75.png) cioè
cioè ![s\ne \sup(f[a,b])](http://upload.wikimedia.org/math/a/0/1/a010cf323783ddfffb2ed8412aa398ec.png) in contraddizione con le ipotesi.
in contraddizione con le ipotesi.Scegliamo, inoltre, una successione
![t_n \in [a,b]](http://upload.wikimedia.org/math/f/7/5/f751b0c29458ad8da51b9a271ce623b9.png) tale che f(tn) = yn.
tale che f(tn) = yn.Per il teorema di Bolzano - Weierstrass (tn) ha una sottosuccessione
 che converge verso
che converge verso ![x_2 \in [a,b]](http://upload.wikimedia.org/math/8/1/b/81bf19383e8ed5a5676f94b71900b44a.png) .
.Per la continuità di f abbiamo
 per
per  .
.D'altra parte
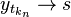 per
per  .
.Quindi per l'unicità del limite abbiamo s = f(x2), cioè la funzione ha in x2 un massimo assoluto.
Similmente si dimostra anche l'esistenza di un punto x1 dove la funzione assume il valore minimo.

Nessun commento:
Posta un commento