Sapere dalla rete: agosto 2011

martedì 30 agosto 2011

luoghi di roma

Roma ha tantissimi luoghi di interesse da non perdere tanto che per vederli tutti sarebbe necessario fermarsi a Roma per più anni ! I monumenti più conosciuti e visitati sono il Colosseo, la Basilica di San Pietro ed i Musei Vaticani, Piazza di Spagna, il Pantheon, la Fontana di Trevi e Piazza Navona. Se volete vedere altri monumenti la lista di tutte le grandi chiese e basiliche, musei, piazze, vie e siti storici che potranno essere di vostro interesse durante il vostro soggiorno nella città eterna.
Al vostro arrivo vi daremo una piantina della città per aiutarvi a orientarvi, ed il nostro personale qualificato sarà sempre a disposizione per tutte le vostre richieste e sarà lieto indicarvi la strada più facile per raggiungere i luoghi di interesse e da visitare

Teorema di Weierstrass

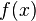Sia $f:[a,b] \to \R \!$ una funzione continua, allora $f(x) \!$ assume massimo e minimo nell'intervallo $[a,b] \!$ .

Dimostrazione con la nozione di compattezza

Poiché $f \!$ è una funzione continua, essa trasforma insiemi compatti in insiemi compatti. Dato che $[a,b] \!$ è un intervallo chiuso e limitato per il teorema di Heine-Borel, è un compatto e quindi anche la sua immagine mediante $f \!$ sarà un compatto. Di conseguenza, il codominio di $f \!$ ammetterà massimo e minimo.

[modifica] Dimostrazione con successioni di punti

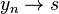Poniamo $s = \sup(f[a,b])$ e individuiamo una successione $y_n \in f[a,b]$ tale che $y_n \rightarrow s$ per $n \rightarrow \infty$ . Questa successione certamente esiste, infatti, se ciò non fosse vero nessuna successione convergerebbe ad

s

, in altre parole, per qualunque

y n

si avrebbe che $\exists \epsilon > 0 \; \forall m \in \mathbb{N} \; \exists n>m : |y_n-s|>\epsilon$ , e d'altra parte, essendo $y_n \in f([a,b])$ allora $\exists \tilde{x}\in[a,b]:f(\tilde{x})=y_n$ per cui avremmo $\exists \epsilon > 0 \; \exists \tilde{x} \in [a,b] : f(\tilde{x}) \ge s+\epsilon>s \; \lor \; f(\tilde{x}) \le s-\epsilon$ cioè $s\ne \sup(f[a,b])$ in contraddizione con le ipotesi.
Scegliamo, inoltre, una successione $t_n \in [a,b]$ tale che

f (t n) = y n

.
Per il teorema di Bolzano - Weierstrass

(t n)

ha una sottosuccessione $(t_{k_n})$ che converge verso $x_2 \in [a,b]$ .
Per la continuità di

f

abbiamo $y_{t_{k_n}}= f(t_{k_n})\rightarrow f(x_2)$ per $n \rightarrow \infty$ .
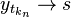D'altra parte $y_{t_{k_n}} \to s$ per $n \rightarrow \infty$ .
Quindi per l'unicità del limite abbiamo

s = f (x 2)

, cioè la funzione ha in

x 2

un massimo assoluto.
Similmente si dimostra anche l'esistenza di un punto

x 1

dove la funzione assume il valore minimo.

Teorema di Laplace

Il teorema di Laplace, per la sua importanza, merità di essere trattato distintamente.

Teorema 45 La somma dei prodotti degli elementi di una linea di una matrice quadrata $A\in K^{n,n}$ per il loro rispettivo complemento algebrico è uguale al determinante di :

$\displaystyle det(A)=\sum_{k=1}^{n}a_{ik}A_{ik}=\sum_{k=1}^{n}a_{kj}A_{kj}\quad (\forall i,j=1,2,...,n)$

Più che una vera e propria dimostrazione, tenteremo di dare un'idea di essa.

Dimostrazione 34 Il determinante si può scrivere come

$\displaystyle det(A)=\prod_{k=1}^{n}a_{ji_{j}}$

Se $i_{1}=1$ allora

$\displaystyle det(A)=a_{11}[\sum (-1)^{r}\prod_{j=2}^{n}a_{ji_{j}}]+a_{12}[\sum (-1)^{r}\prod a_{ji_{j}}]+...$

Ma i termini in parentesi quadre, si verifica che coincidono con i complemento algebrici degli elementi anteposti ad ogni prodotto. Si verifica che la parità è comunque rispettata e pertanto il teorema è stato 'dimostrato'.

Il lettore capirà che sviluppare tale dimostrazione in maniera meno rigorosa è un grande risparmio di calcoli.

Corollario 2 La somma dei prodotti degli elementi di una linea per i complementi algebrici di un'altra linea è nulla:

$\displaystyle \sum_{k=1}^{n}a_{ik}A_{jk}=\sum_{k=1}^{n}a_{ki}A_{kh}=0\quad (\forall i,j=1,2,...,n:i\neq j\neq h)$

teorema di Lagrange

la dimostrazione algebrica ed il significato geometrico, con le conseguenze del teorema di Lagrange. Il significato geometrico che viene dato al teorema di Lagrange è di facile comprensione in quanto fa riferimento al concetto di tangente in un punto. Il teorema si riesce a dimostrare algebricamente facendo riferimento al teorema di Rolle, per cui la funzione di cui si parla risulta costante con derivata prima uguale a zero

Enunciato: data una funzione f(x) continua in un intervallo [a; b] chiuso e derivabile in (a; b) aperto, esisterà un punto x0 appartenente ad (a;b) tale che f ' (x0)=[f(b)-f(a)]/(b-a).

Dimostrazione algebrica: posto g(x)=f(x)-{f(a)+[(f(b)-f(a))/(b-a)]*(x-a)}, calcolando il valore g(x) quando x=a ed x=b, troveremo che g(a)=g(b)=0. Da tale relazione sapendo che la funzione g(x) è continua e derivabile in un punto e imposto che g(a)=g(b)=0, per il teorema di Rolle la funzione è costante con derivata prima uguale a zero. Quindi avremo g '(x)=f '(x0)-[f(b)-f(a)]/(b-a); ciò comporta che f '(x0)=[f(b)-f(a)]/(b-a). La tesi proposta nell'enunciato risulta quindi dimostrata.

Significato geometrico: il significato geometrico che viene dato al teorema di Lagrange è di facile comprensione in quanto fa riferimento al concetto di tangente in un punto. Se un arco di curva è dotato di tangente, esisterà un punto x0 dove la tangente è una retta parallela alla secante che congiunge i due estremi della funzione (o anche arco di curva) dato.

1° Corollario: se in tutto l'intervallo (a; b) si suppone f '(x0)=0, allora la funzione f(x0) è costante in (a; b).

Dimostrazione: prendiamo un qualsiasi punto x0 dell'intervallo (a; b) con x0¹a ed applichiamo il teorema di Lagrange alla funzione in questione nell'intervallo (a; x0). Si ha: [f(x0)-f(a)]/(x0-a)=f '(z) [2] con a

2° Corollario: se in un intervallo (a; b) la derivata f '(x) è sempre positiva, allora la funzione è crescente in tale intervallo; se invece è negativa, la funzione è decrescente.

Teorema di Rolle.

Teorema di Rolle:

Sia y = f(x) una funzione definita e continua nell’intervallo chiuso [a,b] e derivabile nell’intervallo aperto (a,b) e tale che f(a) = f(b), allora esiste almeno un punto c dell’intervallo aperto (a,b) tale che f’(c) = 0.

Dimostrazione

Poiché la funzione y = f(x) è continua nell’intervallo [a,b] per il teorema di Weierstrass[1] essa è dotata di massimo (M) e di minimo assoluto(m) in [a,b]. Indichiamo con x₁ ed x₂i due punti di [a,b] tali che f(x₁) = m ed f(x₂) = M (con m ≤ M).

Per continuare la dimostrazione distinguiamo due casi:

PRIMO CASO.-
Se M = m (cioè il massimo e il minimo assoluto coincidono) allora la funzione è costante nell’intervallo (a,b) e il teorema è dimostrato ricordando il fatto che la derivata di una funzione costante è sempre zero.

SECONDO CASO.-
Se f(x₁) = m < M = f(x₂), osservato che per ipotesi è f(a) = f(b) segue che almeno uno dei punti x₁ ed x₂è interno all’intervallo (a,b).
Infatti, se, per esempio, x₁ coincide con a, segue che x₂è interno ad (a,b) non potendo essere x₂= b in virtù dell’ipotesi f(a) = f(b).
In formule possiamo dire che:

Analogamente si ragiona supponendo x₁ = b, o iniziando il ragionamento con x₂.
In definitiva, almeno uno dei punti x₁ ed x₂è interno all’intervallo (a,b). Sia allora, ad esempio, x₂tale punto, che per quanto suddetto (teorema di Weierstrass) è anche un punto di massimo relativo, e dato che per ipotesi la funzione f(x) è derivabile in (a,b) segue, per un teorema di analisi matematica[2], che in tale punto la derivata è zero: .
Quindi il teorema è dimostrato assumendo c = x_2.

Scomposizione

Sia dato un polinomio P(x), ed un binomio divisore della forma (x-a), con a un numero reale qualsiasi. Sia Q(x) il quoziente. Dalla relazione fondamentale della divisione possiamo dedurre :

Quando R=0 si dice che il polinomio P(x) è divisibile per x-a e la relazione precedente ci fornisce una sua scomposizione in fattori.
Il problema diventa allora quello di trovare i binomi del tipo x-a.
In questo ci aiutano il teorema di Ruffini ed il criterio di divisibilità già visti a suo tempo.

Si può procede nel seguente modo

Si determinano i divisori del termine noto p_i

Si determinano i divisori del coefficiente del termine di grado massimo q_i

Si trovano tutte le possibili frazioni p_i /q_i.Tra questi valori ci sono gli a cercati

Si applica il teorema del resto verificando per quali binomi del tipo x-a è divisibile P(x)

Dopo aver trovato un divisore si esegue la divisione utilizzando la regola di Ruffini

Se necessario si ripetono le operazioni fatte eliminando però i fattori x-a che non hanno dato esito positivo al primo tentativo

Esempio

Si vuole fattorizzare il polinomio

Seguiamo lo schema

i divisori del termine noto 6 sono ± 1, ± 2, ± 3, ± 6,

i divisori del coefficiente del termine di grado massimo 2 sono ± 1, ± 2,

le possibili frazioni sono ± 1, ± 2, ± 3, ± 6, ± 1/2, ± 3/2, di conseguenza i possibili divisori sono

Applichiamo il teorema del resto

e allora x-1 non è divisore

e allora x-1 è divisore
allora il polinomio P(x) è divisibile per x+1

Eseguiamo la divisione utilizzando la Regola di Ruffini.

Ottenendo la scomposizione

Per procedere nella scomposizione in fattori , occorre ora operare sul trinomio

Poiché nessuno dei procedimenti usuali per i trinomi è applicabile, si ripete su di esso il procedimento di Ruffini a partire dal punto 1.

I possibili divisori sono gli stessi del passaggio precedente, con esclusione di x-1 che aveva già dato esito negativo

Applichiamo il teorema del resto.

.........................................................................
Trovato un divisore ripetiamo allora la divisione ottenendo

quindi complessivamente

Da notare che prova Q(-1) poteva anche essere evitata perché assegnando alla x un valore negativo tutti i termini del polinomio diventano positivi.

Teorema di Ruffini

Divisione tra polinomi: Teorema del resto

Il valore che un polinomio in x a coefficienti reali P(x) assume sostituendo ad x il numero a reale è uguale al resto della divisione di P(x) per il binomio x-a.
In particolare il polinomio è divisibile per x-a se e solo se p(a)=0.

Dimostrazione

Dato un polinomio P(x), ed un binomio (x-a), con a un numero reale qualsiasi, dalla relazione fondamentale della divisione possiamo dedurre :

dove Q(x) rappresenta il quoziente ed R il resto, che dovendo essere di grado minore del divisore (x-a) sarà di grado 0, cioè non conterrà la variabile x.
Poiché la relazione vale per ogni valore di x sostituendo la x con a si ottiene :

Cioè la tesi.

Teorema di Ruffini
Il teorema del resto ci permette di stabilire un importante criterio di divisibilità tra polinomi che è di verifica immediata :

Condizione necessaria e sufficiente affinché un polinomio P(x) sia divisibile per un binomio (x-a) è che P(a)=0.
a viene anche detto zero del polinomio.

Criterio di Ruffini

Sia il polinomio P(x) a coefficienti interi; allora se esiste un valore razionale p/q che sostituito ad x annulla il polinomio sarà :

	p divisore del termine noto
	q divisore del coefficiente del termine di grado massimo

In particolare se il termine di grado massimo ha coefficiente unitario il valore che annulla il polinomio sarà un numero intero divisore del termine noto.